MIT Mini Cheetah的关节驱动器为何选用减速比为6的单级内嵌式行星减速器?
今年年初,MIT的Prof. Sangbae Kim课题组发布了开源版本的Cheetah Mini,作者之前做过一些初步的介绍:
https://zhuanlan.zhihu.com/p/58077049
因为Cheetah Mini的开源性质,给了我们很多硬件设计、框架搭建以及运动控制的启发与借鉴,很多同行在汲取精华的同时, 可能都会有一个相对共性的问题——为什么这个关节驱动器选用了6为减速比的行星减速箱?这个 G=6 是不是什么magic number?
那么作者将在本文中,结合Benj的硕士论文以及自己掌握的信息和知识,对其关节驱动器各部件的选型(尤其是减速箱的设计)做一个梳理解读。
在我们解读其减速比为6的单级内嵌式行星减速器之前,我们有必要从头去梳理一下其关节驱动器中各部件的选型动机——这样我们才能有一个更为完整的认识。
关节驱动器选型的逻辑整理
- 应用场景所要求的驱动器性能
在做具体选型之前,我们首先需要明确:四足机器人下的应用场景特征对驱动器的性能要求。简要总结可包括如下五点:1)高频动态响应能力;2)精确力反馈能力;3)低成本实现能力;4)一定的负载能力;5)紧凑的轴向空间实现能力。接下来具体解读各个性能点对驱动器各部件带来的选型要求。
- 高频动态响应能力:【小于60的减速比减速箱+物理高刚度】
为了使四足机器人的整体运动性能呈现高动态性,即我们说的高频动态响应能力好,需要求相应的驱动关节呈现两个特征:1)输出速度高;2)力/位响应的通频带宽。对应到具体的驱动关节参数上,即为1)需使用较低减速比的减速箱(一般需至少控制在60以内);2)物理结构上呈现高刚度,即无柔性元件。
第1点所要求的高频动态响应能力,实际上就已经剔除了现在工业机械臂上,高减速比谐波减速器的驱动器方案,同时也祛除了科研界人形机器人中常用的串联弹性驱动器(SEA)方案,并将减速比限定在60以内。
- 精确力反馈能力 + 3. 低成本实现能力:【小于30的减速比减速箱+电流环力反馈】
为了更好地与外界物理环境进行交互,需要求关节驱动器具备精确的力反馈能力。
首先基于现有的力测量方案与第1点提到的高刚度物理结构,我们只能在:1)电流环;2)应变片中进行选择。其次考虑到低实现成本的因素,我们只能选择更加廉价且方便的电流环方案(应变片以及相应的机械结构载体一般实现成本会在千元级别)。
而在电流环测量力(扭矩)的基础上,为了减小减速箱难以建模的静摩擦力(启动扭矩)给精确测量力带来的负面影响,至少应当选取30以下减速比。作者实际测试过在36减速比下,电流环做精确力控的性能——结果四个字:差强人意。因此简单地定量来说,30的减速比可能会是使用电流环做精确力控的上限。
第2点与第3点所要求的精确力反馈能力与低成本的实现,框定了电流环力反馈的方案,同时也进一步地缩小了减速比的范围,即30以内。
- 一定的负载能力:【力矩电机】
虽然说四足机器人相对于双足人形的尺寸和重量都较小,但毕竟也是归于腿足式机器人的范畴,自然对相应的负载能力,即关机驱动器的输出扭矩有一定的要求。
在已经使用小减速比减速箱的前提下,电机的选型自然而然会倾向于扭矩输出能力强,但转速较低的力矩电机上。这边提供一个大致的扭矩参考数值:
12\,kg 级别小尺寸的Cheetah Mini,髋关节pitch方向的驱动器峰值扭矩要在 18\,Nm 左右;而 45\,kg 级别大尺寸的Cheetah 3,髋关节pitch方向的驱动器峰值扭矩要做到夸张的 230\,Nm 左右——相应的四足机器人才可能体现出较强的运动爆发能力。
第4点所要求的负载能力,决定了驱动器中实际的电机要选定扁平状力矩电机的方案。
关于力矩电机的一些特征,可参考:https://zhuanlan.zhihu.com/p/90120480
- 紧凑的轴向空间实现能力:【外转子+内嵌式单级行星减速器(G<10 )】
在第4点中提及到使用了力矩电机,为了充分利用好力矩电机扁平化、具有充裕的镂空径向空间的特性,自然而然就会想到把减速箱内嵌到此空间内,以最大化地减小驱动器的轴向空间。这里做一个简单的解释,我们常见的在工业机械臂上长筒状的关节驱动器,使用的是最常规的无框电机与谐波减速器的头尾串联式排布,可能在谐波的末端还会再继续串联力矩传感器,这样的结构带来的结果就是轴向尺寸过长。而减速箱内嵌相当于牺牲了径向空间,而在轴向空间上则将减速箱和电机“重合”起来——紧凑的轴向空间可以给腿足机器人整体的躯体设计带来方便,往后的运动性能上带来低惯量的优势。
确定减速箱内嵌的方案之后,在固定的定子线圈的直径下,选取外转子(永磁体)的方案能够尽可能地给减速箱带来较大的径向排布空间。
同时,在力矩电机较短的轴向空间下(一般<20\,mm ),最合适的减速箱方案为单级的行星减速箱。相应的解释如下:在第2&3点中提及到了,为了用电流环精确测量力而使用的小于30的减速比,基本可排除使用谐波的可能性,同时出于成本和非高精度的考虑,也无需使用到摆线针轮,因此成本低且结构简单的行星减速箱无疑更加合适。而在很小的轴向尺寸下,一般只能采用单级的方案,且相应具体的减速比一般会小于10,否则太阳轮、行星轮和外齿圈的直径比例会很奇怪。
第5点所要求的紧凑的轴向空间实现能力,决定了外转子+内嵌式单级行星减速箱的方案,这符合第3点实现成本低的要求,同时单级行星减速箱带来的10以内的减速比则更响应了电流环精确力反馈的方案——即较小的减速比下,静摩擦力负面影响会更小,测量结果更加精准。
- 选型总结
结合以上5点的分析,外转子力矩电机+内嵌式单级行星减速器(G<10 )+电流环力反馈,会是相应四足机器人理想的驱动器设计方案之一。
- 补充问题
Q:能否考虑去除减速箱,仅使用电机直驱?
A:还是需要集成一定减速比的减速箱,去降低齿槽转矩(Cogging)的负面影响。
以上也是一个较为常见的问题——我们是否可以完全丢弃齿轮箱,使用更为强力的力矩电机,这样结构的实现能够更加简单、紧凑、成本更低,同时电流环测量扭矩的结果也更加精准。
答案是不推荐这么做的。首先不谈相应的扭矩输出密度( Nm/kg )的性能会被削弱,更为主要的考虑是:机器人关节的输出转速并不要求那么高,反而绝大部分都是处于低速大扭矩的工况,因此需要串联相应的减速箱去抬高电机端的转速,以降低Cogging效应的负面影响。
关于齿槽转矩(Cogging),详情请戳:https://zhuanlan.zhihu.com/p/90120480
具体减速比“6”的来源
关于最终的这个减速比数字6的来源,作者仔细阅读了Benj硕士论文的Section 2.2.2 Housing and Planetary Gearbox,认为这个减速比6的得来主要有如下3个原因:
- 几何尺寸限制:力矩电机中线圈定子 55\,mm 的内直径;
- 10以内更倾向大减速比的选择:以提升输出能力并降低Cogging负面影响;
- 降低成本:选用Misumi的标准正齿轮,相应on-stock的齿轮型号就决定了具体数值;
我们知道,单级行星齿轮箱的减速比为:
G = 1 + \frac{R_{r}}{R_{s}}\,\,\,\,\,\,\,\,(1) ,其中 R_{r} 为外齿圈半径, R_{s} 太阳轮半径。
首先,从第1点提到线圈定子的内直径为 55\,mm ,再加上减速箱需遵循内嵌于定子的设计理念,因此有 2R_{r}<55\,mm 的关系,Benj在具体实现中选取了 R_{r} = 25\,mm——很自然的选择,因为需考虑到内齿圈一定的高度去做具体的机械实现。
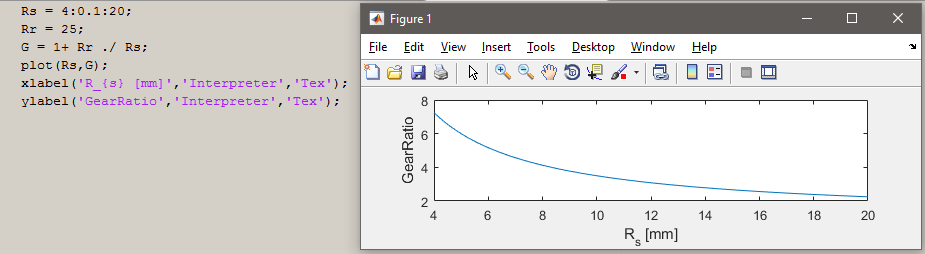
接着,为了满足第2点提到的取得较大的减速比 G ,从公式 (1) 可知太阳轮的半径 R_{s} 需要尽可能的小。可参考下图,当太阳轮半径在 R_{s}\in[4,20] 时,相应的减速比 G\in[2.25,7.25] 。
再接着,基于第3点提到的降低成本(降低成本是Benj做Cheetah Mini设计的核心理念),在太阳轮的使用上,Benj选择了可以从Misumi廉价买到的正齿轮:
- 太阳轮:Misumi GEABN0.5-20-8-K-4,相应的模数 m=0.5 ,齿数 z=20 ,厚度 B=8\,mm,输入轴直径 D_{in}=4\,mm,即太阳轮半径 R_{s}=\frac{mz}{2} = 5\,mm;
关于这个齿轮的选择,首先是选择了较小的模数和齿数,以确保较小的太阳轮半径R_{s} ,进而得到较大的减速比 G ,其次选择了 8\,mm 的齿厚来确保在较小模数下传递扭矩间的强度(补充:作者查阅了Misumi官网,模数0.5已经达到最小,但齿数还有更小的15齿,但15齿下扭矩传递强度不足,揣测Benj为了安全起见,选择了20齿)。
在该太阳轮的基础上,为了符合外齿圈半径 R_{r} = 25\,mm的齿轮啮合要求,相应的行星轮和外齿圈的选型如下:
- 行星轮:Misumi GEFHB0.5-40-5-8-W3,模数 m=0.5 ,齿数 z=40 ,厚度 B=8\,mm,输入轴直径 D_{in}=5\,mm ,即行星轮半径 R_{p}=\frac{mz}{2} = 10\,mm;
- 外齿圈:KHK SI0.5-100,模数 m=0.5 ,齿数 z=100,即外齿圈半径 R_{r}=\frac{mz}{2} = 25\,mm;
因此,相应的单级行星减速器的减速比最终为 G = 1 + \frac{R_{r}}{R_{s}}= 1+\frac{25}{5}=6。最后,也用如下的一张图来总结一下MIT Cheetah Mini的关节驱动器关于减速箱部分的Specifications:
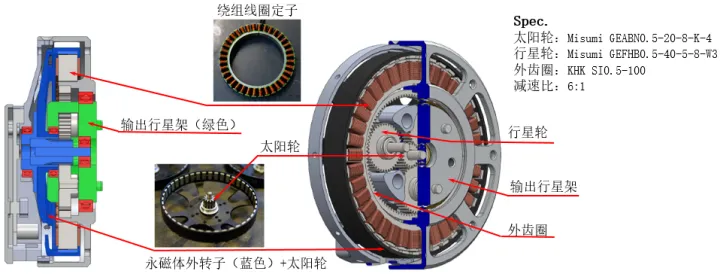
关节驱动器实现方案:外转子力矩电机+内嵌于线圈的单级行星减速器(G=6)+电流环力反馈
以上,即是作者根据Benj的硕士论文以及自己相应的理解,对MIT Cheetah Mini关节驱动器中减速箱部分的设计解读,如有不当需要修改或者需要补充之处,欢迎评论区留言。
最后,要强调一下【原创方案】的可贵与可敬之处。我们很多时候只看到了最后一个成熟可行的方案(比如说这儿用了内嵌单级 G=6 的行星减速箱),就不假思索地copy进行了实现,却忽视了走到最终这个方案背后的思考以及原创者的不懈努力——致敬原创、开源精神的MIT Cheetah Group,Respect!