为什么力矩电机呈现为扁平状?——关于无框力矩电机的一些介绍
最近作者收到了几个共性的问题:
为什么无框力矩电机都是呈现扁平状的物理外形,即径长比(diameter-to-length ratio)较大,这样的设计对比于传统的长筒状无框电机有何优势?
作者将在此文中,通过一些简单的数学分析谈谈自己的看法,有补充和纠正欢迎评论区留言~
(无框)力矩电机,全称应该为永磁无刷直流(无框)力矩电机,其显著的特征是:
- 较大的径长比(diameter-to-length ratio)
- 较多数目的磁极(magnet poles)
这两点确保了其良好的大扭矩输出性能,但同时也呈现较低转速的特性。
这类电机多以无框的形式出现,方便使用者将其集成于相应的机器人关节模组(驱动器)之中——最为典型的为不久前MIT Cheetah团队提出的本体驱动器(Proprioceptive Actuator),相应特点有:
- 一般会集成10以内小减速比的减速箱,进一步去符合机器人低速大扭矩的应用特性
- 一般不使用额外的扭矩传感器,通过电流闭环的形式实现力控
- 永磁体可作为内转子(Cheetah初代版本),也可作为外转子(Cheetah Mini版本)
介绍完了无框力矩电机的基本特性,回到文初的问题上,为什么力矩电机多呈现扁平状而非传统的长筒状?如下图对比所示:
 输出扭矩均为4Nm的两款无框电机——长筒状 or 扁平状 ?
输出扭矩均为4Nm的两款无框电机——长筒状 or 扁平状 ?
为了更好的回答这个问题,我们需要从永磁无刷电机的扭矩输出原理来看,即
$$
\tau = \frac{R^{2}4\mu{0}k{s}LM_{0}\omega}{Gap+L} ,(1)
$$
其中 R 为转子半径;$ \mu{0}$ 为磁通量与磁场强度的转换系数;$ k{s}$ 为线圈表面电流系数;$ L $为永磁体截面厚度(即外半径与内半径之差);$ M_{0}$ 为径向方向的磁化强度(magnet magnetization)在傅里叶展开的第一项; $\omega$ 为轴向的长度; Gap 为永磁体与线圈之间的间隙长度。
因为我们在这里仅需要对比分析几何尺寸参数对输出扭矩带来的影响,所以我们把 $ \mu{0}, k{s}, M{0} $的乘积写作常量,即$ A = \mu{0}k{s}M{0} $,那么公式(1)可简化成:
$$
\tau = 4A \cdot \frac{R^{2}L\omega}{Gap+L} ,(2)
$$
从公式(2)中我们已经可以得到初步的结论:力矩电机的输出扭矩是正比于转子半径的二次方($R^{2}$ )以及轴向长度( $\omega $),同时与定转子间隙长度($Gap$ )呈反相关关系。相信看到这里已经有很多小伙伴明白为什么力矩电机大多数要做成扁平状了。
为了更直观地去理解$ R $与 $\omega $的取值( $R$ 与$ \omega$ 为转子半径与轴向长度,直接对应电机的物理形状)对力矩输出能力的影响,作者还针对公式(2)做了如下处理,这个处理是建立在如下两个假设之下:
- 因为我们仅考虑$ R$ 与 $\omega$ 取值的关系,作为简化,我们将永磁体截面厚度$ L$ 和定转子间隙$ Gap$ 暂时设为定量;
- 同时假设永磁体的体积$ V$ 一定,永磁体体积有$ V = \pi\omega L (2R-L)$ 的关系。假设$ V$ 为常量——是在我们设计腿足机器人的电机时非常重要的一点,因为我们永远考虑的都是【扭矩/质量】的输出密度的概念,即我们在比较任何参数给电机输出扭矩带来改变的同时,一定要考虑相应的质量(体积),而最好的做法就是保持质量一定;
那么,将 $\omega = \frac{V}{\pi L(2R-L)} $代入公式(2),得到如下的(3):
$$
\tau = 4A\cdot\frac{V}{(Gap+L)\pi}\cdot\frac{R^{2}}{2R-L},(3)
$$
使用Matlab在合理 L 取值范围内跑一下公式(3),得到$ R $与$ \tau $ 的大致关系如下图:
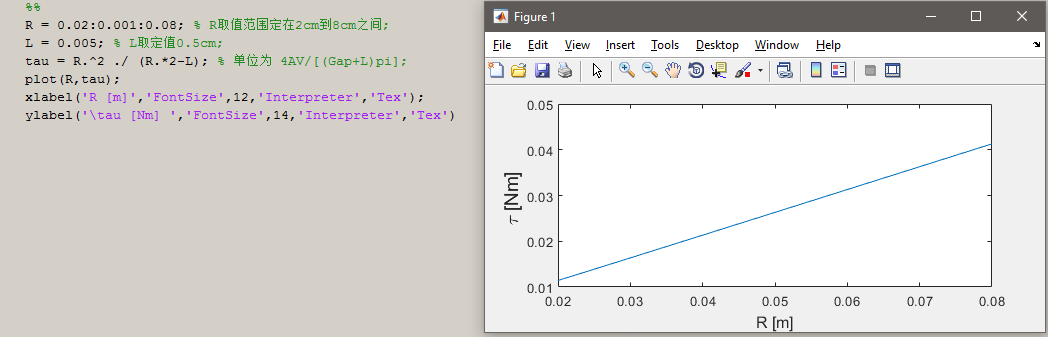
很直观地看出,在永磁体体积$ V $、定转子间隙$ Gap$ 以及永磁体截面厚度 $L$ 一定的情况下,输出扭矩$ \tau$ 和转子半径$ R$ 呈现正相关关系。
提高转子半径$R$ 的大小(永磁体体积一定的情况下,轴向长度 $\omega$ 将取较小值),可以有效地提高电机输出密度的性能。当然因为实际硬件实现以及机器人本身关节尺寸的要求,这个 R 的取值是有相对应的上限(诸如$ \omega$ 太小,定子的绕组、支撑轴承就很难实现)——但也足够去解释为什么力矩电机会呈现径长比( $\frac{2R}{\omega} $)较大的扁平状。
当然,在我们选定固定 R 值的基础上,也可以去比较一下 $\omega$ 与$ L$ 的取值关系对输出扭矩密度的影响(即转子半径 R 、永磁体体积$ V$ 、间隙 $Gap$ 为定值)。将公式(3)做一些细小的改写,得到公式(4):
$$
\tau = 4A\cdot\frac{R^{2}V}{\pi}\cdot\frac{1}{(Gap+L)(2R-L)},(4)
$$
使用Matlab在合理$ Gap$, $R$ 范围内跑一下公式(4),得到$ L$ 与 $\tau $的大致关系如下图:
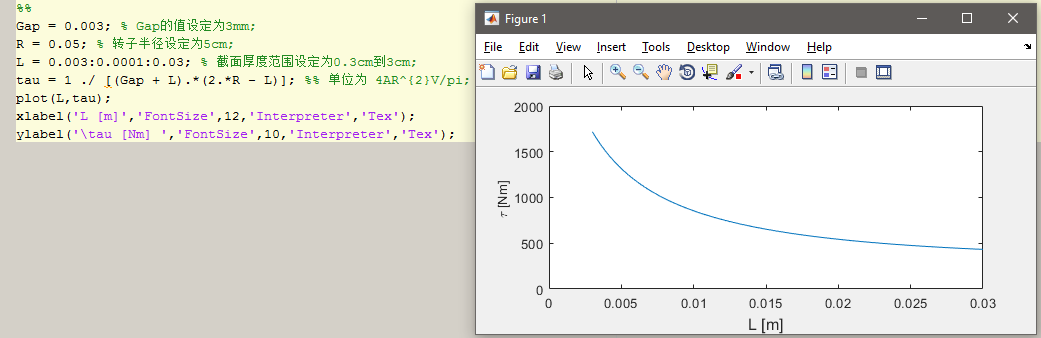
可以看出,为了得到较大的扭矩 $\tau$ 值,永磁体截面厚度$ L$ 值需要尽可能的小,在保持体积 $V$ 一定的情况下,轴向长度 $\omega$ 在这里反而是大的(注意这和之前的结论并不矛盾,这里是在定值 $R$ 的情况下,比较了$L$ 与$ \omega$ 的关系)。
结论:
简要地来讲,为了保证力矩电机呈现较好的【扭矩/质量】的输出密度性能,需要选取较大的永磁体转子半径$ R$ ,较小的截面厚度$ L $与较小的轴向长度 $\omega $。以上参数的选择则对应了其物理形状特征——扁平状与较大的中空镂空。一般的经验之谈,外转子原理的径长比$\frac{2R}{\omega}$ 在$ [7,11] 之间。
延伸:QDD原理的驱动器在双足人形应用的可能
可以说近年来无框力矩电机的广泛使用,使得半直驱原理(QDD, Quasi-Direct-Drive)的关节驱动器在四足机器人领域大展风头——MIT Cheetah系列、宇树科技的AlienGo&Laikago、云深处的绝影系列、前沿驱动INNFOS的新四足等,都采用了QDD原理或者类似的关节驱动方案,相关的优点我不在此文中赘述。
既然QDD在四足领域大获成功,作者想在这里延伸讨论一下,QDD有无在双足仿人(全尺寸,双臂无自由度缺失)领域应用的可能,主要的讨论点在于【峰值输出扭矩及其相应的密度】——这是QDD原理一直被诟病不足的地方,如果这个问题能够得到良好的解决,那么也就没有高减速比谐波原理的驱动器什么事了。如下,作者做一个简要的关于输出扭矩及密度的推算:
在现有电机材料的技术条件下,永磁体转子的【扭矩/体积】的输出密度一般在
$$
\tau_{v} = [60, 100]kNm/m^{3},
$$
我们考虑一个正常(较大)双足机器人关节驱动器的永磁体转子空间
$$
R = 0.05m; L = 0.03m; \omega = 0.04m,
$$
那么理想情况下该力矩电机的最大的输出扭矩在
$$
\tau{max} = V\cdot\tau{v-max} = \pi\omega L(2R-L)\cdot\tau_{v-max} = 26.39Nm,
$$
考虑到QDD方案会集成一个减速比较小的齿轮箱,我们在这里假定减速比为 G = 10 ,一切理想情况下的峰值扭矩在 $$
\tau{max-actuator} = \tau{max} \cdot G = 263.9Nm,
$$
这个数值似乎是能符合一个双足人形髋、膝和踝关节pitch方向,大家常谈的约 $200Nm$ 的峰值扭矩要求——但这是不准确的,$ 200Nm$ 的这个数值一般是针对整机自重在 $80kg$ 左右的全尺寸人形。
接下来我们可以看看采用上述QDD方案下机器人的自重,首先是单个永磁体转子的自重
$$
m_{rotor} = \rho\cdot V = \rho \cdot \pi\omega L(2R-L) = 1.98kg\rho = 7500kg/m^{3},
$$
考虑使用外转子方案+驱动器轻量化做到无可挑剔——我们把关节驱动器的重量设定为永磁体转子的2倍,那么相应的【峰值扭矩/质量】的输出密度就在:
$$
\tau{max-density} = \frac{\tau{max-actuator}}{2\cdot m_{rotor}} = 66.67Nm/kg,
$$
这个峰值扭矩的密度与MIT Cheetah 2所使用的驱动器密度类似( $60.41Nm/kg$ )。对比而言,任意一款集成高减速比谐波减速器的关节驱动器,其输出密度是能够轻易做到$150Nm/kg$ 以上。
更为直观地来说,我们搭建一个全尺寸人形机器人,即使去除末端执行器和头部的自由度,还是需要基本的27个关节单元(双腿【6 x 2】+ 双臂【 7 x 2】+ 腰部【1】),而单单这27个QDD的质量就要达到 $108kg $——这是无法控制到在$80kg$的自重的,因此之前谈的 $200Nm$ 的峰值扭矩要求也无从说起(实际峰值扭矩的要求将随着自重而水涨船高)。
结论:
QDD方案目前是无法胜任全尺寸双足人形的【扭矩/质量】的输出密度要求(争议较大,作者个人观点)。对于高减速比谐波的驱动器方案,诚然有着动态能力差、结构复杂与成本高的劣势,但其扭矩输出密度还是杠杠的。
所有问题的核心是永磁体转子的【扭矩/体积】的输出密度$ \tau_{v} $这一数值,即 $100kNm/m^{3} $的扭矩体积密度还不够大到免除减速箱的地步。我们永远玩的都是在扭矩和角速度之间tuning传动比的trade-off。QDD在四足领域成功的本质是针对低负载、低惯量但对动态性能要求高的应用场景,做了牺牲负载能力但提高高频响应、降低成本与简化机械结构的驱动器方案——已然是足够耀眼的工作。
对于QDD在双足人形的应用,作者是持比较保守的态度,诚然也看到过一些QDD在双足人形上的尝试,但私以为是”讨巧“的做法——非全尺寸或者缺乏上身自由度。不过,机器人领域永远是demo说话,我也了解到一些优秀的学者对此有不同的看法,也希望早日能够被"打脸"以提高自己的姿势水平~